1. はじめに
ライフ・ゲームってご存知ですか?
ライフ(life)を日本語訳したら「人生ゲーム」みたいですが、そうではありません。ライフ・ゲームとは、ホートン・コンウェーさんが考えたシミュレーションの名前です。 このシミュレーションでは、碁盤のようなマス目がそれぞれ生命体であると考え、それぞれが状況に応じて生まれたり死んだりします。
ライフ・ゲームのルールをもう少し詳しく説明しておきましょう。
あるマス目について周囲に3個のライフがあれば、そこにライフが生まれます。 そして、周囲に2個のライフがあれば、そのマス目に変化は生じません。
でも、それ以外の場合には、そのマス目のライフは死んでしまいます。 たとえば周囲に4個とか5個のライフがあると窒息してしまうし、周囲に誰もいないと寂しさに耐えられない、といったイメージです。ルールはこのように非常に単純なのに、初期のライフの分布に応じて様々なパターンが生じることから、ライフ・ゲームは当時、爆発的な人気が出たそうです。
そしてこのライフ・ゲームは、コンピュータの父と呼ばれるフォン・ノイマンさんによって考案されたセル・オートマトン(cellular automaton)という考え方に則っています。
セル・オートマトンは、「平面上に細胞のように配置された単位オートマトンが、それぞれ自己と近傍の状態のみに従って内部状態を変え、系全体の動きを定める」として定義されています。 ここで、内部状態が「生きている・死んでいる」の2パターンだけで考えると、たしかにライフ・ゲームになりますね。ところで、生物の骨は力学環境の変動に応じて、再構築(リモデリング)により機能的に適応変化する、と言われています。 これについて、骨を細かいサイコロ状に区分して考えてみましょう。 力学環境が変化すると、それぞれのサイコロは自分や周囲に加わる力が変わり、それに応じて適応変化している、と考えることができるのではないでしょうか。
これって、内部状態が「とても強い・強い・普通・弱い・とても弱い」のような、いくつかのパターンでできたセル・オートマトンであると言うことができそうです。この研究では、セル・オートマトンの考え方を応用して、力学環境に適応した構造物の自動生成を試みています。 そして、力学環境に適応する骨体の形状をセル・オートマトンモデルで表現できないか探っています。
(骨の適応変化については、「構造物を構築するセルロボット」でもうちょっと詳しく述べています。)2. 手法の流れ
あたりまえな話なのですが、力学環境に適応した構造物をセル・オートマトンモデルで生成するためには、力学環境が構造物に与える影響を知る必要があります。 私達は有限要素法と呼ばれる手法を用いてこれを解析しています。
有限要素法では解析したい対象物を細かいメッシュに分割し、それぞれの箇所に生じる応力の分布を求めることができます。 セル・オートマトンも、単位オートマトンと呼ばれるものが並んだメッシュ構造であるため、有限要素法による解析に適しています。解析ではまず、同一形状・同一物性の要素(セル)を多数並べた構造物に対して有限要素解析を行います。
そして、そこで求まる応力分布に応じて各セルの物性値を変更します。
物性値が変更された構造物について再び有限要素解析を行って各セルの物性値を変更します。 さらにこの構造物について有限要素解析を行い、ということを繰り返すことによって、最終的に得られる構造がどのようになるかを調べます。具体的な処理の流れは次の通りです。
- 初期条件を設定する
解析対象の初期形態と、その対象物を細分化したセルが活動できる領域を設定します。 かつては2次元問題を主に取り扱ってきましたが、最近は計算機性能があがったので、3次元問題を多く行っています。 私達は細かい立方体形状のセルを多数並べて作られる、非常に単純な初期形態で解析を始めています。
- セルに働く荷重と境界条件(拘束条件)を与える
力学解析を行うためには、力の加わる箇所と大きさ、そしてどこか固定された箇所(拘束条件)が必要となります。 どこかを固定してあげないと、力を加えても、その方向にそのまま移動してしまって、解析を行うことができなくなってしまうからです。
- 応力状態を計算する
有限要素法を用いて現在の構造物に生じる応力の分布を求めます。 そして、その結果から、それぞれのセルに生じている応力値を算出します。
- 応力を評価する
各セルに生じた応力値を評価します。 高い応力が生じているセルはもっと強化する必要がありますし、応力が低いセルならもっと弱くても良いし、場合によってはいらないのかもしれません。
- ヤング率を変化させる
強化や弱化は、材料の物性値の一つであるヤング率と呼ばれる数値を変更することによって表現します。 ヤング率は値が大きいと材料が固くて強いことを意味し、小さければ柔らかい材質となります。
現在は300種類ほどのヤング率を事前に用意し、得られた応力値に応じてこのうちから適したものを選ぶ、という手法でヤング率を変化させています。 ただし、ヤング率を大幅に変更してしまうと、構造がなくなってしまう可能性があります。 そのため、元のヤング率から徐々に変更しなければなりません。
- 手順(2)に戻る
これまでの手順を何度も何度も繰り返します。 ヤング率を1ステップで変更する度合などにもよりますが、100回程度繰り返すことによって形状はほぼ安定します。
3. 解析結果
シミュレーションの結果得られる構造について、いくつかご紹介します。
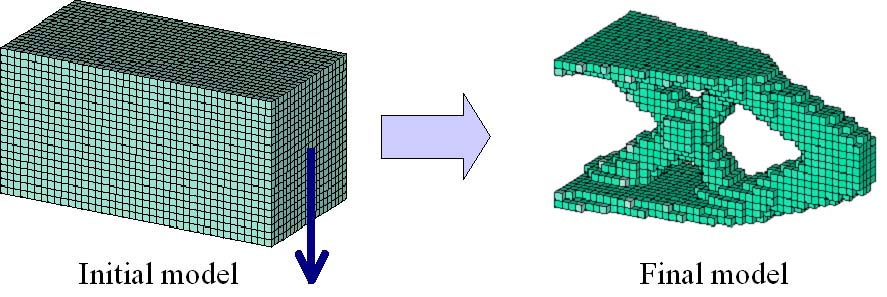
まず一つ目はとても単純なモデルで、壁から生えた四角柱の端っこに力が加わっている状態です(下図左)。 この状態を初期状態として上記手法でシミュレーションをしたところ、下図右のような構造が得られました。
外側が三角形になるだけでなく、内部にX型の柱ができていることによって、たしかに丈夫そうな構造になっています。
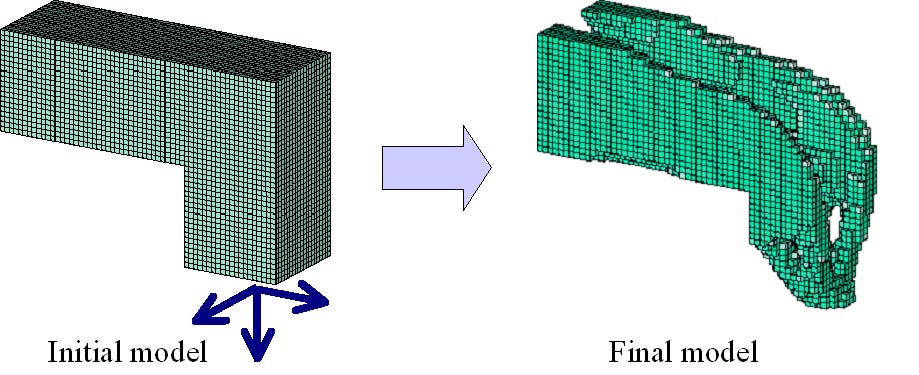
二つ目はもうちょっと複雑なモデルです。 今度は下図左のように壁からL字型をしたものを生やし、その一部に3方向の力を加えてみました。
複数の力を同時に加えたのでは、合力として斜め方向の力と同じことになってしまいます。 そこで、それぞれの力の方向について解析を行い、どの荷重方向にも適応するように工夫して生成したモデルが下図右です。
角柱の真ん中がすっぽり空洞になっているのがなかなか興味深いところです。
4. 今後の予定
はじめに述べたように、生物の骨も力学環境に適応していると考えられており、私達はそれをセル・オートマトンモデルで表現したいと思っています。 そこで現在は、生物の力学状態を単純な初期モデルに与えて、骨体形状の生成を試みているところです。(初稿 2002年4月 小関道彦)